编码
编码的意义重大,一个好的编码不仅仅能够提高工作效率,数据安全等更重要的是能够带来重大的社会益。以床染病检测为例,在重大突发公共卫生事件中,首要的就是检测出感染人群,切断传播链,那么时间无疑是最宝贵的。人们如何在还未出现新的传播链之前,在最短时间之内检测出人群中的感染者,隔离传播源、切断传播链条是首要解决的问题。若有 100 人需要检测,将100人编号 00 - 99,以最方便的核酸检测为例,10 人混检。按照一般的方法只需要检测 10 份即可,但是这样如果某一份中出现了阳性并不能定位到个人,那么需要对这 10 人重新检测,但是在上次检测到下次检测之间的这段时间,病毒可能会随着人员的流动而传播开来,进而形成新的传播链条。现在的方法是对 00 - 99 进行编组,共计编为20组,个位数字 0 - 9 共计 10 组,十位数字 0 - 9 共计 10 组,总计公 20 组,在第一次采样时候就对每个人采样两份,分别放入个位 数字的组中和十位数字的组中,以下图中的 10 号为例,采样两份分别放入 行组的第一组和列组的第零组中,即 [10, 11, 12, 13, 14, 15, 16, 17, 18, 19] 这10人为 1 组,[00, 10, 20, 30, 40, 50, 60, 70, 80, 90] 这10人为一组,假设这20人中只有10一人为阳性,那么必然导致行组中的第1组为阳性,列组中的第0组为阳性,由此,仅一次检测便可定位到单个被感染的人,大大提高了切断病毒传播链的可能性。当然如果有多人阳性,那么必然引起其他各检测行组和列组的检测结果阳性。
| 0 | 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 2 | 20 | |||||||||
| 3 | 30 | |||||||||
| 4 | 40 | |||||||||
| 5 | 50 | |||||||||
| 6 | 60 | |||||||||
| 7 | 70 | |||||||||
| 8 | 80 | |||||||||
| 9 | 90 | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
数据校验
目的:解决编码在时间、空间上传输的可靠性。时间传输可靠性即1年前存入硬盘的数据1年以后还能读出,并且和存入数据保持一致;空间传输可靠性指的是在信源发出的信息通过信道到达信宿能够被正确还原,即发送方发送什么,接收方就接收什么。
常用校验方法如下:
奇偶校验:编码中1的个数的奇偶性
海明校验:多组奇偶校验,检错码为出错位
CRC:循环冗余校验
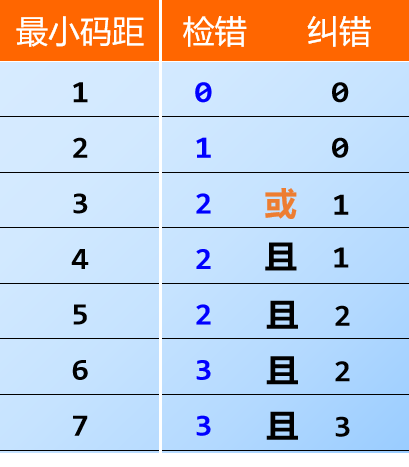
码距:任意两个合法编码之间不同的二进制位数,码距越大,抗干扰能力了、纠错能力越强,数据冗余越大,编码效率越低。奇偶校验最小码距为2,海明码最小码距为3
最小码距≥e+1可检测e个错误
最小码距≥2t+1 可纠正t个错误
最小码距≥e+t+1e>t 可纠正t个错误,同时检测e个错误
偶校验
校验码(数据+校验位)中1的个数为偶数,冗余位 1,校验位 P,P 表示编码中为1的位数,以3位二进制编码为例
\[P = D_1\bigoplus D_2 \bigoplus D_3 \bigoplus D_4\]| 十进制原码 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 二进制原码 | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 校验码 | 0000 | 0011 | 0101 | 0110 | 1001 | 1010 | 1100 | 1111 |
校验码(数据+校验位)中1的个数为偶数,冗余位 1,校验位 P,P 表示编码中为1的位数,以3位二进制编码为例
奇校验
校验码(数据+校验位)中1的个数为奇数,冗余位 1,校验位 P,P 表示编码中为1的位数,以3位二进制编码为例
\[P =\overline{ D_1\bigoplus D_2 \bigoplus D_3 \bigoplus D_4}\]| 十进制原码 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 二进制原码 | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 校验码 | 0001 | 0010 | 0100 | 0111 | 1000 | 1011 | 1101 | 1110 |
显然奇偶检验码能够检测出奇数个bit位置出错,但是不能检测出偶数个bit位置出错。接收方在接收到发送方发来的数据后进行计算
\[G = P_1 \bigoplus D_1\bigoplus D_2 \bigoplus D_3 \bigoplus D_4\]若,G = 0则数据大概率正常,若G = 1则数据一定出错
二维奇偶校验
对数据直接进行奇偶校验能够检测出奇数个bit错误,但不能检测出偶数个bit错误,不能定位到出错的bit位置。如何改进奇偶校验使得计算机能够检测出错误bit的位置,由此引出了二维奇偶校验。对数据进行分组,每n个数据位增加一个校验位,同时对于整个数据增加1个n + 1 位的数据校验位,如下图所示,每7bit数据增加1bit校验位,同时对整个数据包增加8bit的校验位。
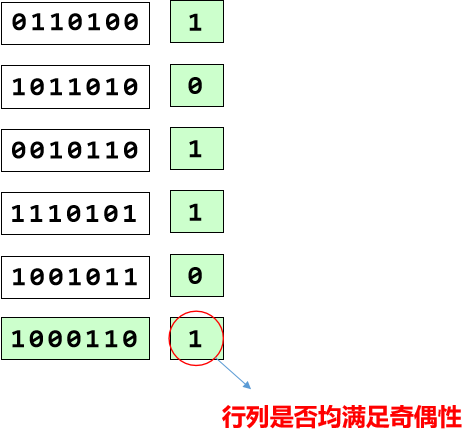
对于1位bit错误可定位到该位的位置进而纠错
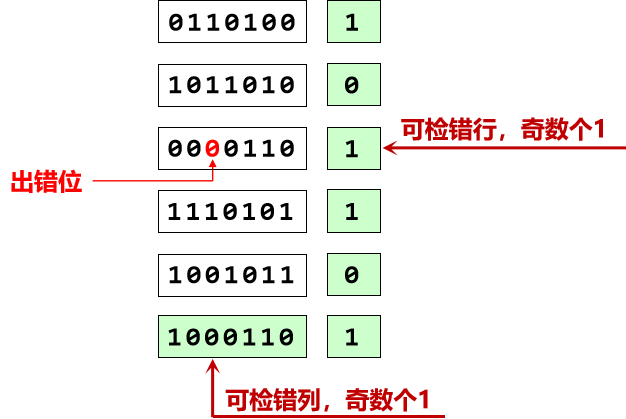
对于两位bit错误,均可检错但不一定能纠错
如下图只能定位到出错的列但是无法定位到出错行,进而无法纠错
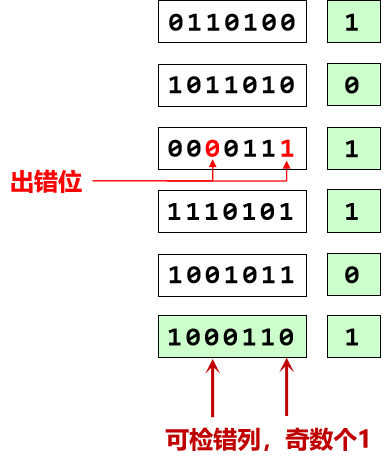
但是如果是出于不同行或者不同列的两位错误可以检错也可以纠错
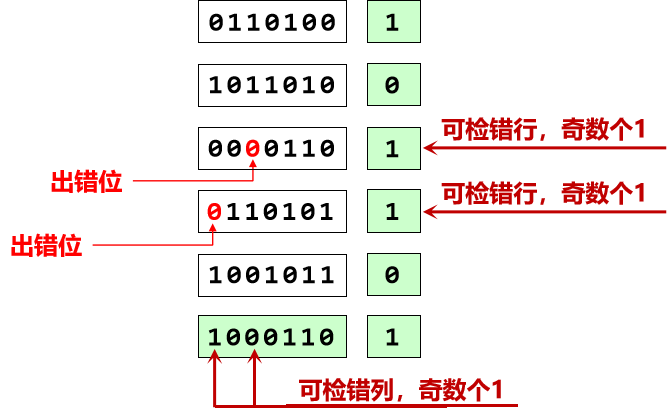
对于3位bit错误,均可检错但不一定能纠错
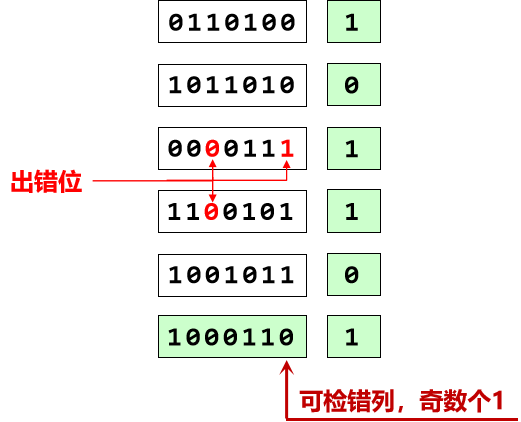
对于4位bit错误,均可检错但不一定能纠错
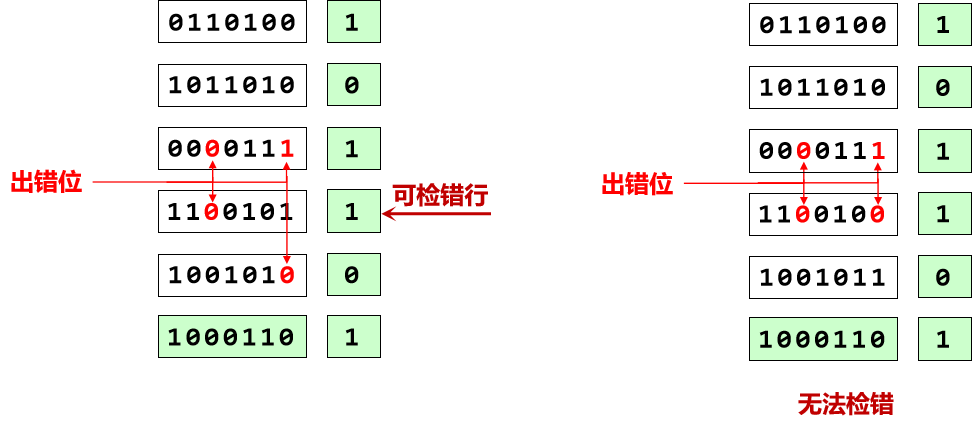
综上,二维奇偶检验的核心是让一个数据位参加多个校验组,一个数据位发生错误可以在多个检测码中反映出来,可以有效提高检错能力。
海明校验
基于多组奇偶校验的启发出现了海明校验。海明校验的本质就是分组奇偶校验。
- 待编码数据分成 r 个奇偶校验组, r > 1, 若 r = 1,那么就是简单的奇偶检验
- r 个校验组有 r 个校验位, 生成 r 个检错码
- 每个数据位至少参加 2 个校验组, 一个数据位出错,可导致多个检错码为1
- 检错码的值表示出错的位置,检错码全零标书数据正常,最低位是1开始, 因为 0 已经用于表示数据正常,可检错也可以纠错(假设一位bit出错,必可纠错)
设海明码 N 位,其中数据位 k 位,校验位 r 位 (冗余位)
\[N = K + r < 2^r -1\]减一是因为全零表示数据正常
以4位数据位为例(7,4)海明码 r = 3,数据位\(D_i\)校验位\(P_i\)是如何映射到海明编码中的位置的
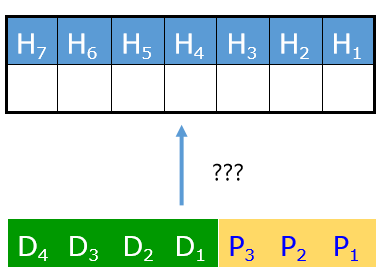
检错码的值表示出错的位置
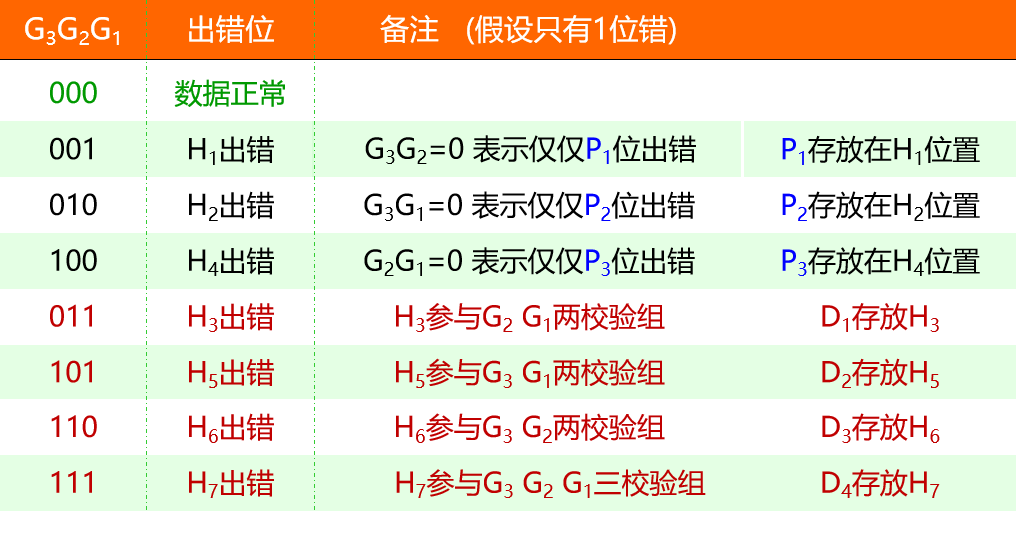
分组关系用图表示如下
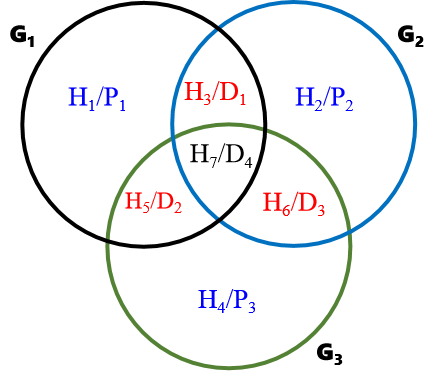
G1(P1,H3,H5,H7)
G2(P2,H3,H6,H7)
G3(P3,H5,H6,H7)

于是得到如下数据位\(D_i\)校验位\(P_i\)是映射关系
G1=P1⊕D1⊕D2⊕D4
G2=P2⊕D1⊕D3⊕D4
G3=P3⊕D2⊕D3⊕D4
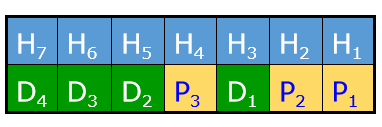
综上:
假设只有一位bit错误,海明码可检一位错,可纠一位错
检错码\(G_3G_2G_1 ≠000\),值为出错位置,取反即可纠错
可检出两位错,但是无法对两位错误进行纠错
假设D1 ,D2同时出错,即H3和H5同时出错, \(G_3G_2G_1 ≠110\) ,但是实际出错位置并不是H6
大多数三位数错误都能检测
如果D1,D2,D3同时出错 \(G_3G_2G_1=000\) ,但是数据并不是正确的
如何区分一位错和两位错误进行纠错
引入总偶校验位,同时假设没有三位bit错误
总偶校验位\(P_4 = H_1 \bigoplus H_2 \bigoplus H_3 \bigoplus H_4 \bigoplus H_5 \bigoplus H_6 \bigoplus H_7\)
若\(G_4 = P_4 \bigoplus H_1 \bigoplus H_2 \bigoplus H_3 \bigoplus H_4 \bigoplus H_5 \bigoplus H_6 \bigoplus H_7\)
\(G_3 G_2G_1\) G4 result 000 0 数据正常 \(\not=000\) 0 数据2bit错误 \(\not=000\) 1 数据1bit错误